Parte do senso comum costuma difundir a ideia de que nas ciências humanas haveria uma comunidade científica sem consenso metodológico e factual em contraste, por exemplo, com as ciências naturais; ou, de modo mais moderado, possuiria pouco consenso. E há ainda quem, incluso dentro das academias, compactuando com tal senso, considere, em contraposição, que é positivo e interessante às humanidades que não haja um endurecimento e uma padronização tal na comunidade sob pena de se perder assim a riqueza de diferentes pontos de vista sobre um objeto de estudo que, em si mesmo, enquanto fenômeno humano, seria já ambíguo e/ou complexo; seja ele uma relação de trade-off entre inflação e desemprego (em Economia)1, a existência ou não da terceira pessoa (em Linguística)2 ou a questão da autoria das obras de Shakespeare (em História)3. Por um lado, há uma boa justificação em se ver tal lado positivo para as ciências humanas; positivo enquanto ganho crítico em contraste com uma mera operação técnica em cima de um paradigma consolidado, para utilizar os termos de Thomas Kuhn. E não a esmo na Alemanha do séc. XIX tais ciências eram chamadas “ciências do espírito” (Geisteswissenschaften), ciências sempre abertas a uma nova interpretação do objeto-vivo. Mas, também tendo em vista casos de incertezas como os levantados acima em diferentes humanidades, convido os leitores a refletirmos de modo introdutório, breve e conciso sobre um outro lado, sobre a vantagem lógica de se priorizar uma comunidade científica coesa diante de quadros controversos de interpretação dos fenômenos.
Dentro do domínio das Lógicas Modais, há uma lógica chamada lógica epistêmica que se ocupa especificamente de raciocínios com conceitos operacionais de conhecimento/knowledge (K) e crença/belief (B) e traduz formalmente enunciados como os seguintes:
- (i)
- “João sabe que não está morto”;
- (ii)
- “Maria acredita que ‘João sabe que não está morto”’;
- (iii)
- “João está convencido de que não está morto”.
Para tal suponha as seguintes definições de identidade (≡) para os enunciados (i)–(iii):
- ‘João’ ≡ j;
- ‘Maria’ ≡ m;
- “João está morto” ≡ p;
- “João não está morto” ≡ ¬p;
- “estar convencido de que” = “acreditar que sabe que” ≡ BK.
- (i)
- Kj¬p;
- (ii)
- BmKj¬p;
- (iii)
- BjKj¬p.
Ademais, podemos também formalizar princípios epistemológicos, como o seguinte: “se alguém sabe que é o caso que ocorra/exista tal coisa, então tal coisa é o caso”4; ou seja: “para qualquer indivíduo i tal que i saiba que α, então α é o caso”. Se entendermos ‘α’ como uma proposição qualquer, tal como ‘p’ e ‘¬p’, e se entendermos o esquema “se… então…” como uma implicação (→), podemos formalizar esse princípio da seguinte forma:
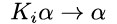
E assim podemos formalizar outros princípios, como “se alguém não acredita que tal coisa, então acredita que não acredita nisso”:
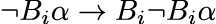
Por conseguinte, em lógica, dizemos que uma expressão do tipo “se… então…” enquanto implicação (→) é válida se sempre que o antecedente for verdadeiro, o consequente também é. Nesse sentido, dizemos que “chuva implica nuvens carregadas” é uma implicação válida porque sempre que é verdade que há chuva, é verdade que há nuvens carregadas. Desse modo, logicamente podemos verificar, por meio de outros princípios previamente aceitos, se um raciocínio epistêmico é válido ou não. Por exemplo: se alguém acredita que acredita em algo, então ela acredita em algo?
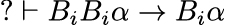
Vamos supor que tal raciocínio não é válido. Se for assim, então há pelo menos uma situação em que o antecedente é verdadeiro e o consequente é falso, o que nos dá, portanto:
- 1.
- BiBiα
- 2.
- ¬Biα
E, se aceitarmos o princípio de que falamos há pouco, temos também
- 3.
- ¬Biα → Bi¬Biα
Ocorre que o antecedente da implicação em (3) é verdadeiro, está na linha (2), logo, podemos deduzir que também é verdadeiro que
- 4.
- Bi¬Biα
Mas, se é assim, da conjunção (∧) entre (1) e (4), chegamos a uma contradição:
- 5.
- BiBiα ∧ Bi¬Biα
Ou seja, “i acredita que acredita que α é o caso e (∧) i acredita que não (¬) acredita que α é o caso”. Ora, se um sujeito i não quiser aceitar contradições em seu raciocínio, precisará, portanto, aceitar que
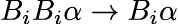
Do contrário, isso o levaria a uma contradição, como vimos. Outrossim, a formalização deste teorema5 pode ser sintetizado como (¬Biα → Bi¬Biα) ⊢ (BiBiα → Biα). Tal expressão indica que, dado que se aceite o princípio ‘¬Biα → Bi¬Biα’, então segue-se dedutivamente que ‘BiBiα → Biα’.
Em suma, a lógica epistêmica serve para formalizar e explicitar as regras e os enunciados epistêmicos que os agentes João, Maria etc. na prática fazem, e tais ferramentas podem ajudar a verificar se seus raciocínios não os levam a contradição. Algumas vezes, o cálculo não é difícil, e a intuição nos bastaria, mas muitas vezes serão inevitáveis o papel e a caneta. Além disso, há um agravante: em geral, os agentes epistêmicos, como, por exemplo, em um conjunto de cientistas, não raciocinam isoladamente, mas cooperam entre si ou inferem algo levando em conta a
crença ou conhecimento de outro, o que lhes ajuda, e muito, para alcançarem suas conclusões, e é aqui que entra a importância de haver uma confiança dentro desse grupo e uma coerência entre seus raciocínios (rejeitando a contradição).
Entendendo essa preocupação, há ramos da lógica epistêmica (como a lógica do anúncio público) que trabalham com raciocínios epistêmicos em contextos em que é relevante o compartilhamento de informações entre os agentes epistêmicos para que cheguem a uma solução razoável. A formalização desses raciocínios em geral é muito complexa para ser introduzida neste breve texto, mas podemos ilustrar seu intento com o seguinte puzzle: Crianças sujas. Três irmãos a, b e c estão distraidamente brincando no quintal quando seu pai os chama para o interior de casa. Após entrarem, dois deles, digamos a e b, estão com as testas sujas de lama, mas não sabem disso. Tampouco c sabe que sua própria testa está limpa. O pai dera antes instruções explícitas para que não se sujassem durante a brincadeira. Obviamente, cada criança conhece o estado em que se encontram as testas das outras duas, mas não a sua própria; porém, a despeito de serem extremamente inteligentes e honestas, devido à proverbial rivalidade entre irmãos, ninguém avisa aos demais sobre a lama em suas testas antes da inspeção paterna.
Ao deparar-se com esse cenário, o pai resolve divertir-se com a situação: “ora, ora, vejo que pelo menos um de vocês está com a testa enlameada… deem um passo à frente aqueles que souberem como estão suas próprias testas!” Os irmãos sabem que seu pai é um homem razoável e nunca agressivo; por isso, estão mais do que dispostos a admitirem sua própria transgressão e suportarem o habitual discurso reprovador. Entretanto, nenhum tem certeza suficiente para dar o passo à frente. Ainda bem-humorado, o pai repete o comando, e apenas os dois culpados avançam. Dirige-se, então, ao terceiro filho que ainda estava em dúvida, e repete: “Avance agora somente se também tiver certeza de como está sua testa!”, e finalmente a criança c dá um passo à frente.
Penso que o principal atrativo dessa historinha se deva à maneira como ela exemplifica de que modo a percepção individual da ignorância coletiva acerca de uma informação pode levar ao conhecimento esperado. Com efeito, uma reflexão cuidadosa do exemplo — a qual deixo para a diversão de nosso leitor — revelará que as reações dos irmãos a, b e c se baseiam em uma série breve de conclusões lógicas a partir das reações realizadas pelo grupo após cada anúncio público do pai.
Vejamos, por fim, uma analogia do anúncio público do pai no puzzle com uma situação concreta entre historiadores. Consideremos a obra grega antiga chamada Biblioteca (Βιβλιοθήκη). Como observou Aubrey Diller (1983), um certo “Apolodoro” é indicado como seu autor em manuscritos sobreviventes, e acreditou-se por um tempo que se tratava de Apolodoro de Atenas (nascido em 180 a.C.), devido a um repertório similar em mitologia. Contudo, logo se observou que o texto cita um autor romano, Castor de Rodes, o qual era contemporâneo de Cícero (século I a.C.); logo, por razões cronológicas, esse “Apolodoro” não poderia ter escrito o livro, e então, por convenção, passou a ser chamado Pseudo-Apolodoro o autor da Biblioteca. Tal “descoberta”, em termos lógico-epistêmicos, traduz-se em anúncio público para a comunidade científica que imediatamente passa a revisar seu conjunto de crenças a respeito das questões que eram então discutidas a respeito dos mais diferentes assuntos entre os agora, reconhecidamente, dois autores distintos. Isso só ocorreu, todavia, porque a comunidade reconheceu a legitimidade do anúncio público; mesmo a parcela da comunidade que não pôde ela própria averiguar diretamente sua pertinência e confiou no anúncio, tal como as crianças no puzzle que não poderiam ver a lama na própria testa, mas confiavam no julgamento do pai.
Assim, terminamos com esse exemplar de como as comunidades científicas em humanidades são capazes de assumir consensos com confiança em métodos e fatos. Tais consensos, quando aliados à busca da coerência entre as crenças individuais — como na demonstração de nosso pequeno teorema —, podem trazer vantagem lógica para chegar a soluções de problemas compartilhados pela comunidade, alguns dos quais não podem ser resolvidos por indivíduos isolados, como vimos no exemplo das crianças.
NOTAS
1Em Economia, denomina-se ‘trade-off’ a uma situação em que há conflito de escolha. Aplica-se comumente em uma ação econômica que visa à resolução de um problema e acarreta outro, obrigando uma escolha. Um caso conhecido em macroeconomia é o da equação da Curva de Phillips, que mostra que uma menor taxa de desemprego leva a um aumento da inflação, e uma maior taxa de desemprego a uma menor inflação. Contudo, esta relação não é válida no longo prazo.
2Émile Benveniste mostrou que as três pessoas em conjugações verbais não possuem o mesmo estatuto. A 1a e a 2a pessoas (‘eu’ e ‘tu’) são sempre participantes da comunicação, mas a 3a (‘ele’) designa qualquer ser ou não designa ser nenhum, e, portanto, seria uma não-pessoa, o que justifica seu uso em expressões como “chove” (em francês, “il pleut”). Essa conclusão da não-pessoalidade, contudo, é questionada ou atenuada por outros autores.
3Recentemente uma nova edição de Oxford da trilogia sobre o rei Henrique VI trouxe Marlowe como coautor junto de Shakespeare e revitalizou o debate sobre se, afinal, as obras de Shakespeare teriam sido escritas por um só autor ou por vários. A inclusão de Marlowe, que até pouco tempo era considerado o rival de Shakespeare, foi o resultado de uma investigação internacional feita por 23 especialistas em cinco países que se utilizaram de métodos tradicionais aliados a tecnologia de ponta para analisar computacionalmente os padrões de linguagem usados pelos dois autores. Entretanto, além das críticas metodológicas possíveis de se levantar a respeito, alguns historiadores defendem que o conceito de autoria no séc. XVI seria muito diferente do conceito atual.
4Exemplos: “Se João sabe que não está morto, então, de fato, não está morto”; “Se João sabe que Maria viajou, então, de fato, Maria viajou”, neste segundo exemplo, se não fosse o caso que Maria viajara e, pois, João estivesse enganado a esse respeito, então acertadamente João não sabia, e sim acreditava que sabia (= estava convencido) que Maria viajou.
5Dizemos que um conjunto de princípios somados a regras de inferência, como a que usamos implicitamente para deduzir (4) desde as linhas (2)–(3), forma um sistema lógico, dentro do qual pode-se provar dedutivamente certos teoremas. Mais particularmente o primeiro sistema de lógica epistêmica foi elaborado por Jaakko Hintikka (1962).
Referências
DILLER, Aubrey. “The Text History of the Bibliotheca of Pseudo-Apollodorus”. In: Studies in Greek Manuscript Tradition. Edited by Aubrey Diller, pp. 199–216. Amsterdam: A. M. Hakkert, 1983.
FEDERAL RESERVE BANK OF BOSTON. Understanding Inflation and the Implications for Monetary Policy: A Phillips Curve Retrospective. Federal Reserve Bank of Boston. Disponível em: <https://www.bostonfed.org/news-and-events/events/economic-research-conference-series/understanding-inflation-and-the-implications-for-monetary-policy-a-phillips-curve-retrospective.aspx>.
FIORIN, José Luiz (org.). Introdução à Linguística: II. Princípios de análise. São Paulo: Contexto, 2012.
ENDRICKS, Vincent; SYMONS, John. “Epistemic Logic”. In: Stanford Encyclopedia of Philosophy (Jan. 4, 2006). Disponível em: <https://plato.stanford.edu/entries/logic-epistemic/>.
HINTIKKA, Jaakko. Knowledge and Belief: an introduction to the logic of the two notions. New York: Cornell University Press, 1962.
KUHN, Thomas S. A Estrutura das Revoluções Científicas. Trad. de Beatriz Vianna Boeira e Nelson Boeira. São Paulo: Editora Perspectiva, 1998.
MORTARI, Cezar A. Introdução à Lógica. São Paulo: Editora Unesp, 2016.
PEREIRA, Márcio Kléos Freire. Extensões de Primeira Ordem para a Lógica do Anúncio Público. Tese de doutorado em Filosofia (Epistemologia e Lógica). Florianópolis: Universidade Federal de Santa Catarina, 2015.
SHEA, Christopher D. “New Oxford Shakespeare Edition Credits Christopher Marlowe as a Co-author”. In: The New York Times (Oct. 24, 2016). Disponível em: <https://www.nytimes.com/2016/10/25/books/shakespeare-christopher-marlowe-henry-vi.html?_r=2>.
[vc_row][vc_column][vc_text_separator title=”SOBRE O AUTOR” color=”juicy_pink” border_width=”2″ el_class=”vc_sep_color_juicy_pink vc_separator-has-text
“][vc_column_text][authorbox authorid = “8”][/authorbox][/vc_column_text][/vc_column][/vc_row]
Vítor Medeiros Costa
Related posts
História da Historiografia
História da Historiografia: International
Journal of Theory and History of Historiography
ISSN: 1983-9928
Qualis Periódiocos:
A1 História / A2 Filosofia
Acesse a edição atual da revista



